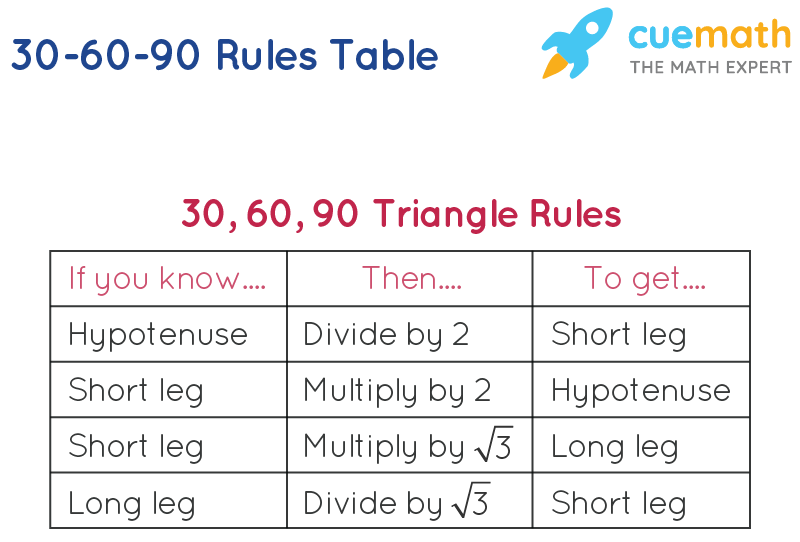
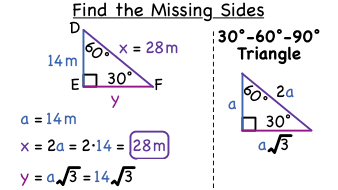
30 60 90 triangle sides If we know the shorter leg length a, we can find out that b = a√3 c = 2a If the longer leg length b is the one parameter given, then a = b√3/3 c = 2b√3/3 For hypotenuse c known, the legs formulas look as follows a = c/2 b = c√3/2 Or simply type your given values and the 30 60 90 triangle calculator will do the rest!While the largest side, 2,A triangle is a special right triangle with some very special characteristics If you have a degree triangle, you can find a missing side
30 60 90 Triangle Piqosity Adaptive Learning Student Management App
What is 30 60 90 triangle
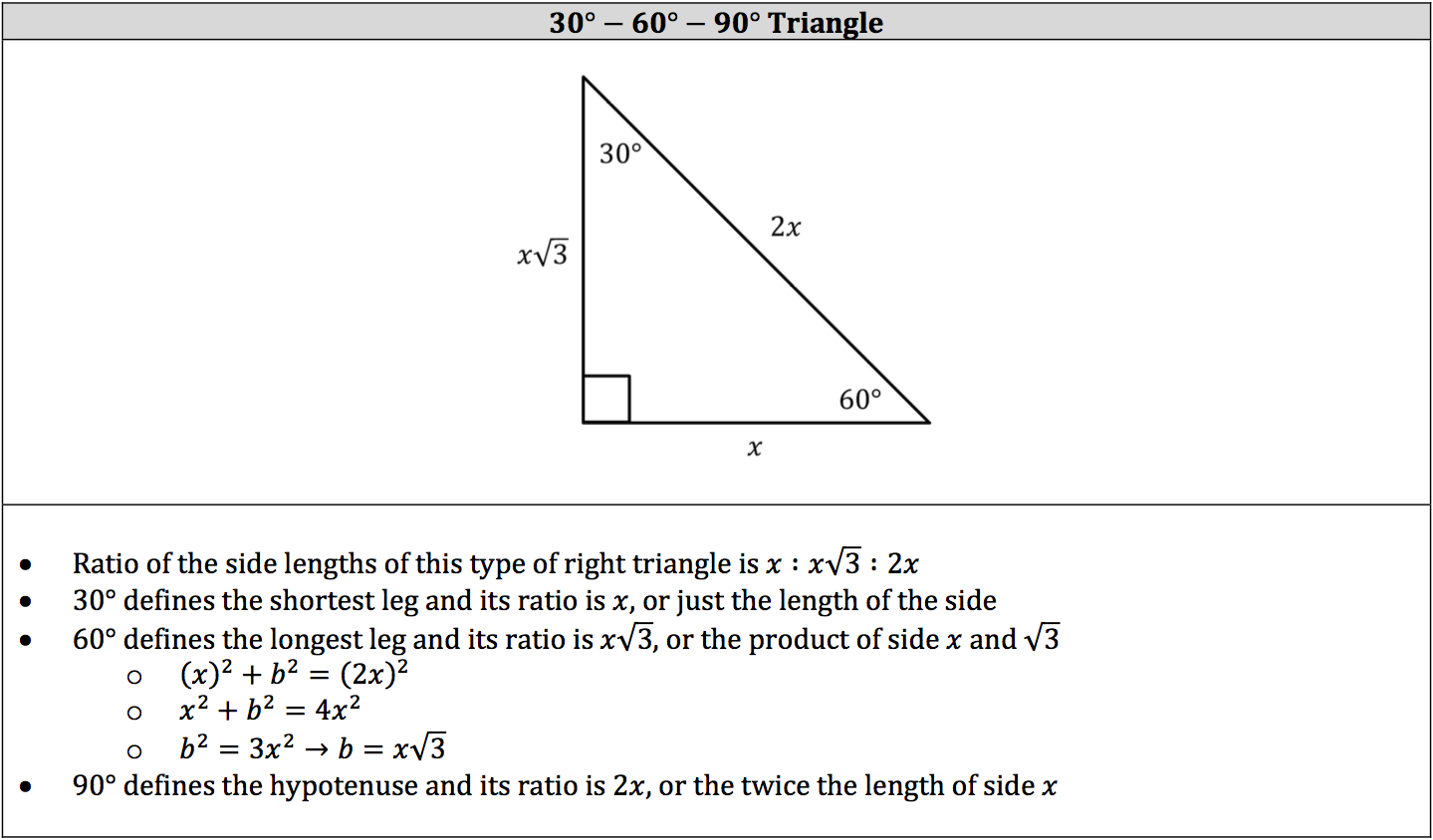
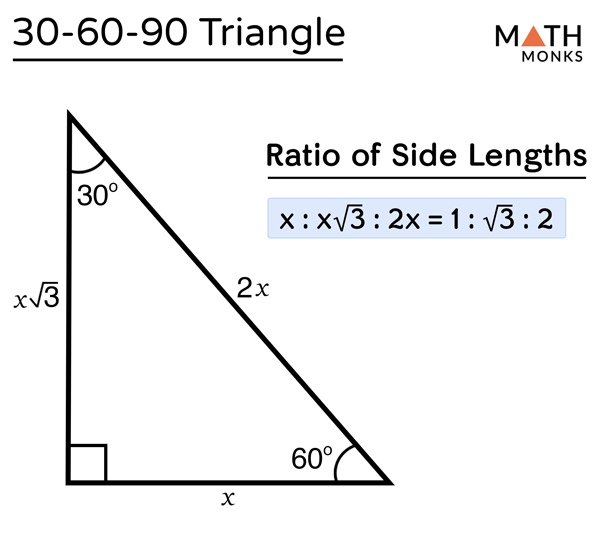
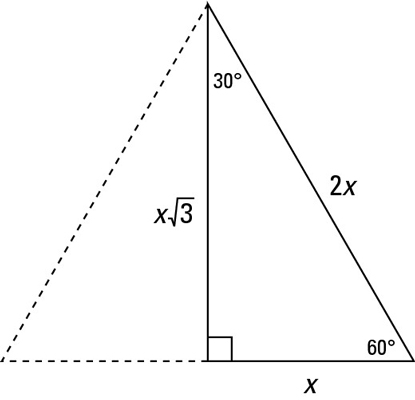
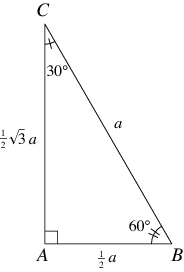
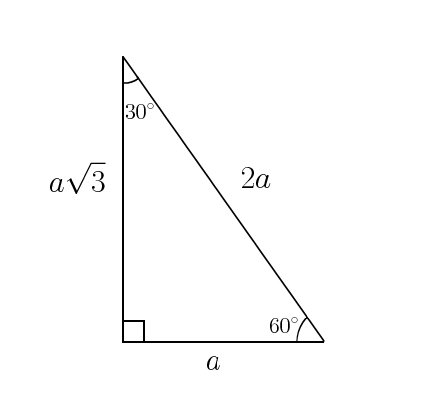
What is 30 60 90 triangle-A 30 60 90 triangle completes an arithmetic progression 3030=6030 =90 An arithmetic progression is a sequence of numbers in which the difference of any two successive numbers is a constant For instance, 2,4,6,8 is an arithmetic progression with a constant of 2The ratio of the sides follow the triangle ratio 1 2 √3 1 2 3 Short side (opposite the 30 30 degree angle) = x x Hypotenuse (opposite the 90 90 degree angle) = 2x 2 x Long side (opposite the 60 60 degree angle) = x√3 x 3



30 60 90 Triangle Geometry Help
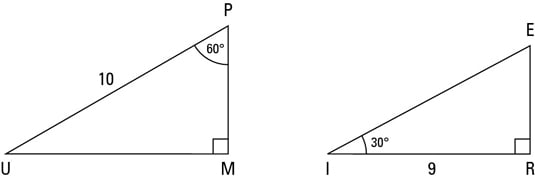
Answer to Find the remaining sides of a 30, 60, 90 triangle if the opposite side of 60 degrees is 6 By signing up, you'll get thousands ofTheorem In a 30°60°90° triangle the sides are in the ratio1 2 We will prove that below (For the definition of measuring angles by "degrees," see Topic 12) Note that the smallest side, 1, is opposite the smallest angle, 30°;It turns out that in a triangle, you can find the measure of any of the three sides, simply by knowing the measure of at least one side in the triangle The hypotenuse is equal to twice the length of the shorter leg, which is the side across from the 30 degree angle
Question Find the remaining sides of a 30°–60°90° triangle if 39 The shortest side is 1 40 "The shortest side is 3 41 The longest side is 8 42 The longest side is 5 43 The longest side is 44 'The longest side is 24 45 The medium side is 3V3 46 "The medium side is 2V3 47 The medium side is 6 48 The medium side is 4A 30 60 90 triangle is a special type of right triangle What is special about 30 60 90 triangles is that the sides of the 30 60 90 triangle always have the same ratio Therefore, if we are given one side we are able to easily find the other sides using the ratio of 12square root of three tan (60) = √3/1 = 173 The right triangle is special because it is the only right triangle whose angles are a progression of integer multiples of a single angle If angle A is 30 degrees, the angle B = 2A (60 degrees) and angle C = 3A (90 degrees)
Answer (1 of 3) If the length of the hypotenuse is given by r, let a = 30 degrees for now x = r*cos a y = r*sin a Then b = 60 degrees, the side between a = 30 degrees and the right angle will be x and the side between b = 60 degrees and the right angle will be y x = r*cos 30 degrees = SQRT(TOPIC 76 30°60°90° TRIANGLES Anytime that you are solving for a missing length in a 30°60°90° triangle, label it like this EXAMPLES What would the labels be for each of the sides of the A triangle is a special right triangle (a right triangle being any triangle that contains a 90 degree angle) that always has degree angles of 30 degrees, 60 degrees, and 90 degrees Because it is a special triangle, it also has side length values which are always in a consistent relationship with one another



5 5 Special Triangles




Special Right Triangles 30 60 90 Ck 12 Foundation
As one angle is 90, so this triangle is always a right triangle As explained above that it is a special triangle so it has special values of lengths and angles The basic triangle sides ratio is The side opposite the 30° angle x The side opposite the 60° angle x *Triangle in trigonometry In the study of trigonometry, the triangle is considered a special triangleKnowing the ratio of the sides of a triangle allows us to find the exact values of the three trigonometric functions sine, cosine, and tangent for the angles 30° and 60° For example, sin(30°), read as the sine of 30 degrees, is the ratio of the sideAs the name suggests, the three angles in the triangle are 30, 60, and 90 degrees As a result, the lengths of the sides in a have special relationships between them that allow you to




30 60 90 Triangle Piqosity Adaptive Learning Student Management App



Triangle 30 60 Calculator Endmemo
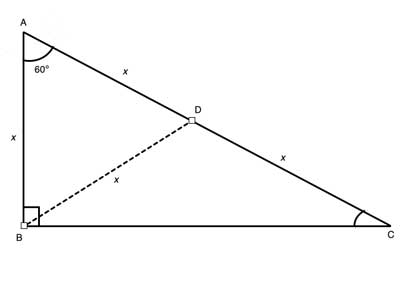
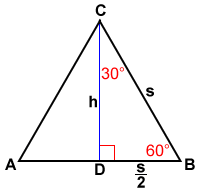
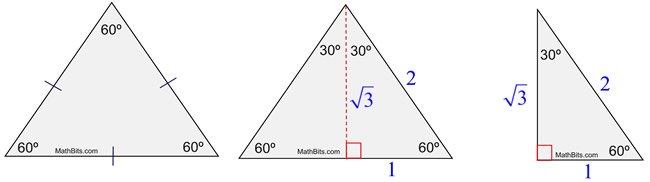
An equilateral triangle bisected by an altitude (its height) creates two 30°60°90° triangles In a 30°60°90° triangle, the longer leg and the hypotenuse are in the ratio Applying this ratio to the triangle, If one side of a triangle is 4, the perimeter is 12 Alternatively, REF 09aThe triangle is called a special right triangle as the angles of this triangle are in a unique ratio of 123 and the sides are in the ratio 1√3 2; A triangle is a special right triangle (a right triangle being any triangle that contains a 90 degree angle) that always has degree angles of 30 degrees, 60 degrees, and 90 degrees Because it is a special triangle, it also has side length values which are always in a consistent relationship with one another




How To Use The Special Right Triangle 30 60 90 Studypug



30 60 90 Triangle
A triangle is a special right triangle that always has angles of measure 30°, 60°, and 90° All the sides of a triangle can be calculated if any one side is givenSo draw a perpendicular to the base, which also bisects both the third side as well as the 1° vertex angle like this It bisects the 1° into two 60° angles like this Let each of the two halves of the third side be x Now for the right triangle on the left Since this is a 30°60°90° right triangle, we know that the shorter leg (theTriangles A triangle is a right triangle whose internal angles are 30, 60 and 90 degrees The three sides of a triangle have the following characteristics All three sides have different lengths The shorter leg, b, is half the length of the hypotenuse, c That is,



The Easy Guide To The 30 60 90 Triangle



30 60 90 Triangle Definition Formulas Examples
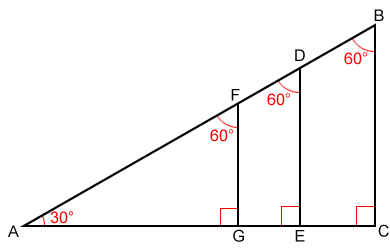
A $$ is one of the must basic triangles known in geometry and you are expected to understand and grasp it very easily In an equilateral triangle, angles are equal As they add to $180$ then angles are are all $\frac {180}{3} = 60$ And as the sides are equal all sides are equal (see image) So that is a $$ triangle The triangle is a special right triangle, and knowing it can save you a lot of time on standardized tests like the SAT and ACT Because its angles and side ratios are consistent, test makers love to incorporate this triangle into problems, especially on the nocalculator portion of the SATThe 45°45°90° triangle, also referred to as an isosceles right triangle, since it has two sides of equal lengths, is a right triangle in which the sides corresponding to the angles, 45°45°90°, follow a ratio of 11√ 2 Like the 30°60°90° triangle, knowing one side length allows you to determine the lengths of the other sides




30 60 90 Triangle Theorem Ratio Formula Video




30 60 90 Triangle Theorem Ratio Formula Video
A special right triangle is a right triangle having angles of 30, 60, 90, or 45, 45, 90 Knowledge of the ratio o 👉 Learn about the special right triangles30°60°90° Right Triangles All 30°60°90° Right Triangles are formed by taking half of a Equilateral Triange, as shown in the steps below Because the original triangle is Equilateral, that means all three sides are the same length This is what variable "x" is trying to tell you All three sides are the same lengthA right triangle (literally pronounced "thirty sixty ninety") is a special type of right triangle where the three angles measure 30 degrees, 60 degrees, and 90 degrees The triangle is significant because the sides exist in an easytoremember ratio 1 √3 3 2 That is to say, the hypotenuse is twice as long as the shorter leg, and



Solution What If The Short Side Of A 30 60 90 Triangle Has A Radical



Why In A 30 60 90 Triangle Is The The Side Opposite 60 Degrees X Sqrt 3 Quora
30 60 90 triangle rules and properties The most important rule to remember is that this special right triangle has one right angle and its sides are in an easytoremember consistent relationship with one another the ratio is a a√3 2a Worksheet 45 ¡45 ¡90 triangleand30 ¡60 ¡90 triangle 1For the 45 ¡45 ¡90 triangle, (the isosceles right triangle), there are two legs of length a and the A is a scalene triangle and each side has a different measure Since it's a right triangle, the sides touching the right angle are called the legs of the triangle, it has a long leg and a short leg, and the hypotenuse is the side across from the right angle A triangle is a right triangle with angles 30^@, 60^@, and 90^@ and which has the useful property of having easily calculable side lengths without use of trigonometric functions A triangle is a special right triangle, so named for the measure of its angles Its side lengths may be derived in the following manner



30 60 90 Right Triangles Consider The Following
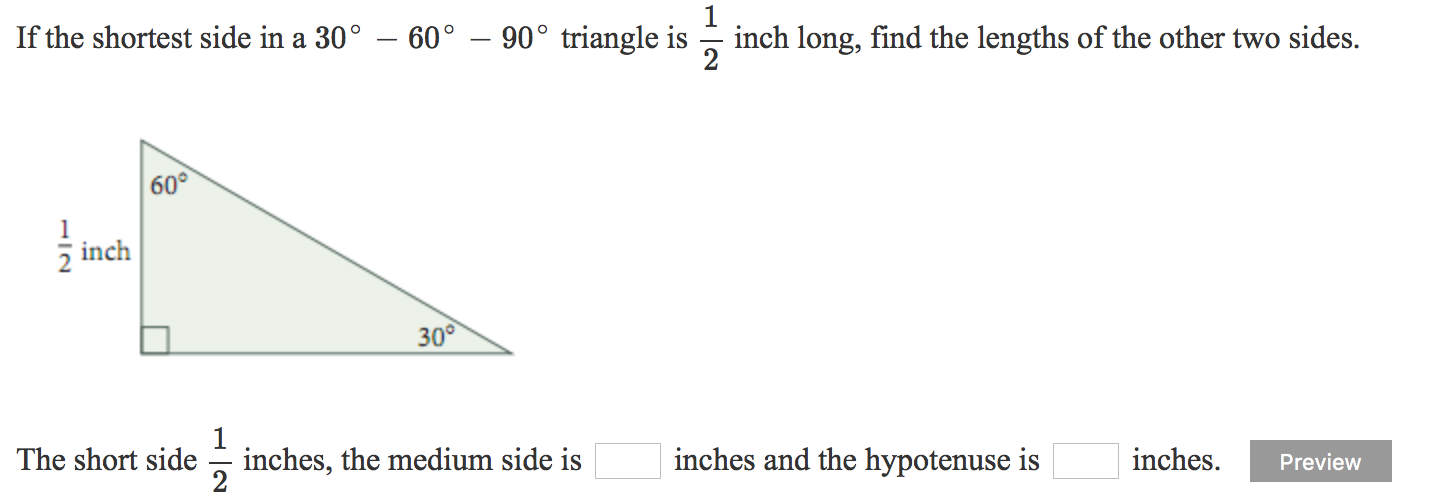



Solved If The Shortest Side In A 30 60 90 Triangle Is Z Chegg Com
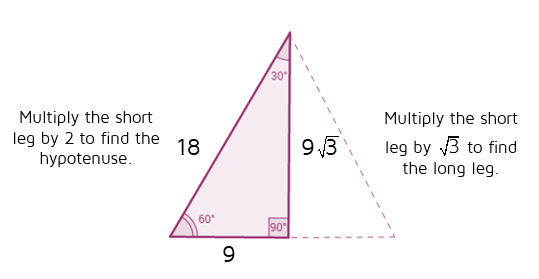



30 60 90 Triangles P4 Kate S Math Lessons




30 60 90 Triangle Theorem Ratio Formula Video



30 60 90 And 45 45 90 Triangle Calculator




30 60 90 Triangles




A Quick Guide To The 30 60 90 Degree Triangle Dummies




The 30 60 90 Triangle Topics In Trigonometry
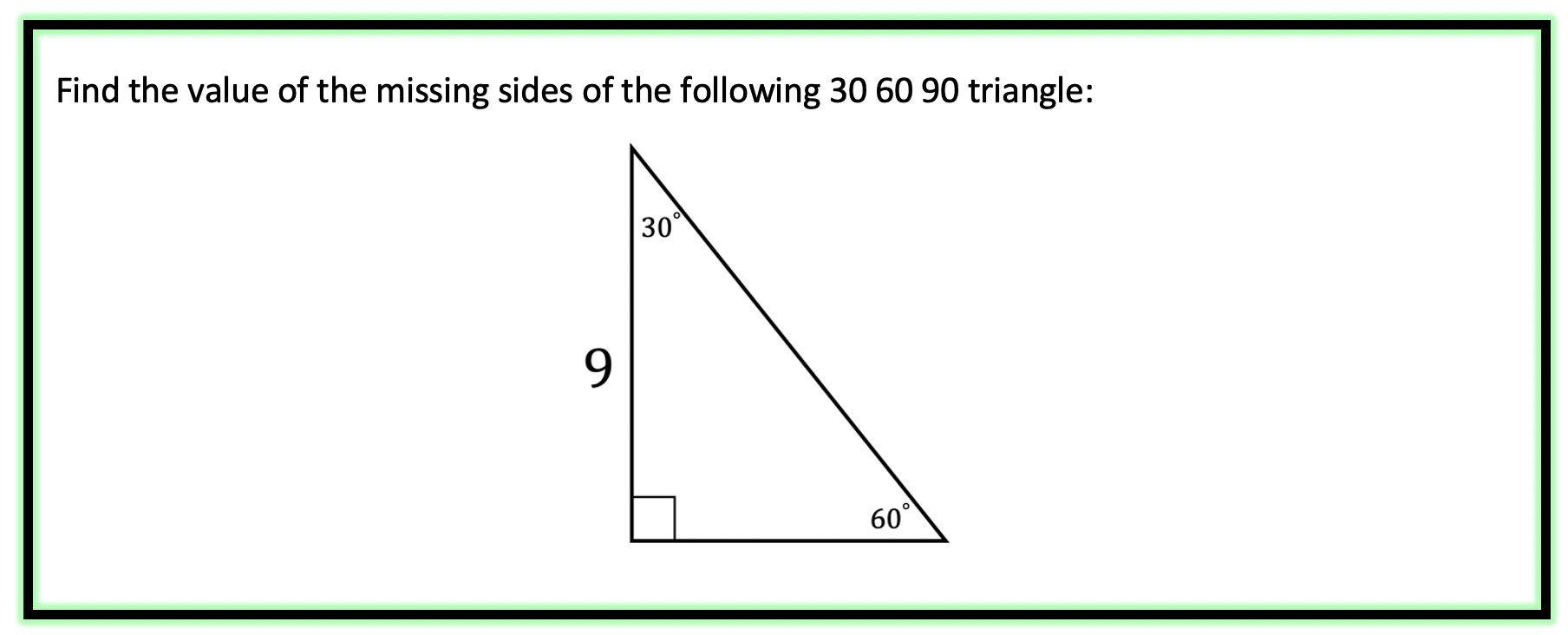



30 60 90 Special Triangles Geometry Mathsux 2
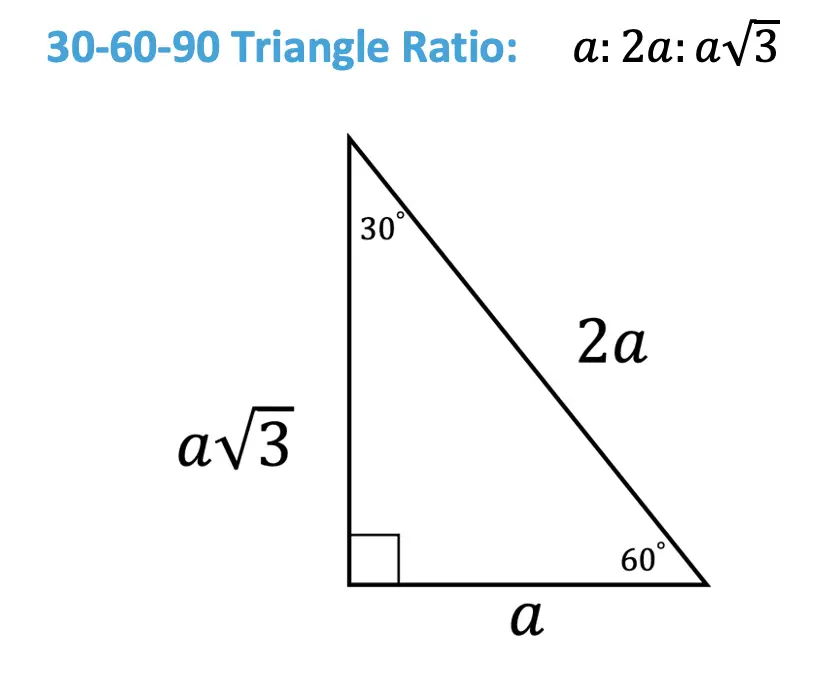



30 60 90 Special Triangles Geometry Mathsux 2
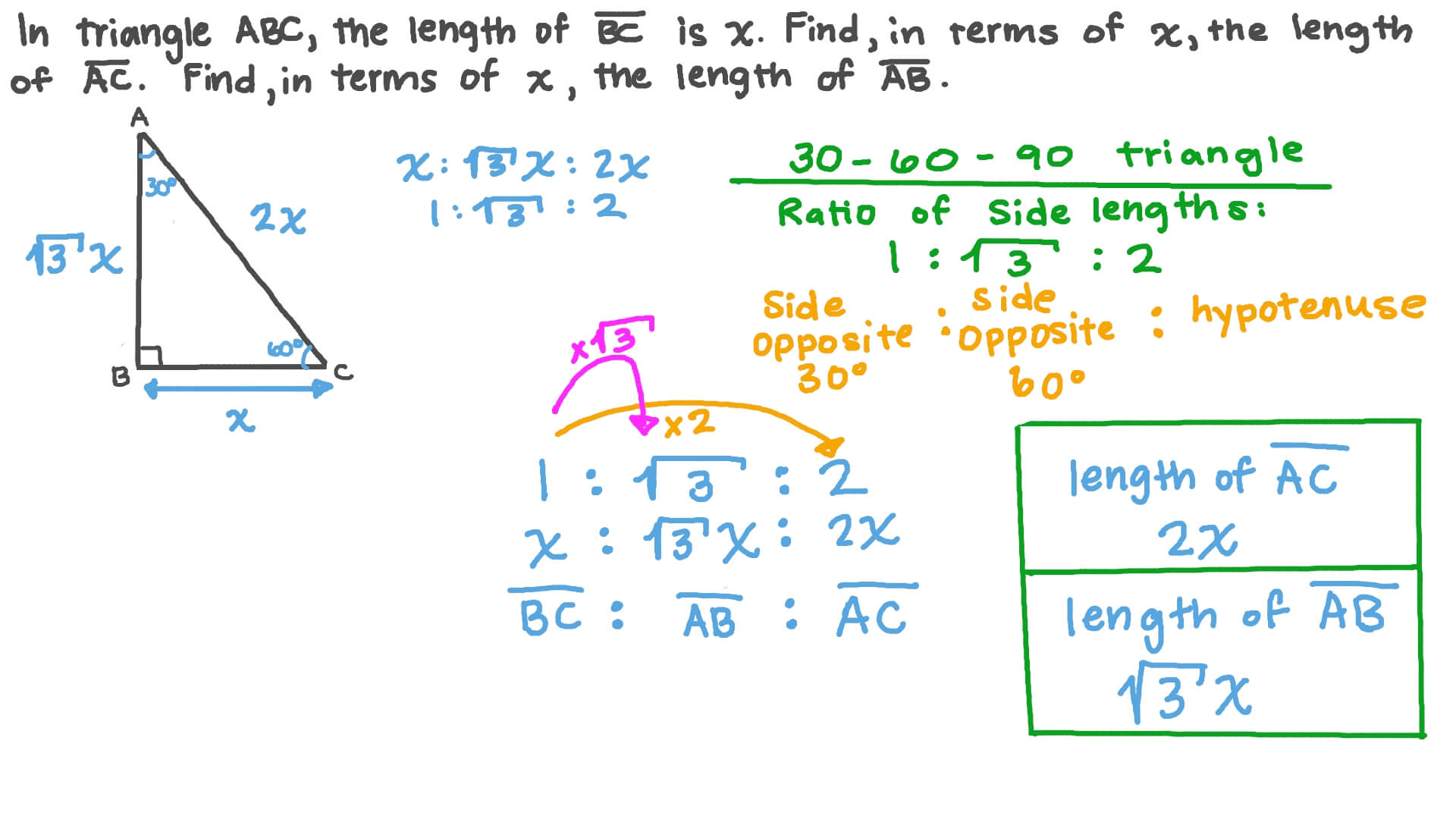



Question Video The Side Lengths Of 30 60 90 Triangles Nagwa




Special Right Triangles Fully Explained W 19 Examples




30 60 90 Triangle Rules Sides Ratio Of A 30 60 90 Triangle Video Lesson Transcript Study Com




Special Right Triangles Proof Part 1 Video Khan Academy




30 60 90 Special Right Triangle Calculator Inch Calculator
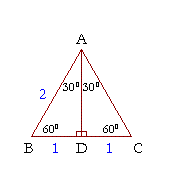



30 60 90 Right Triangle Side Ratios Expii




Relationships Of Sides In 30 60 90 Right Triangles Ck 12 Foundation




30 60 90 And 45 45 90 Triangles Youtube
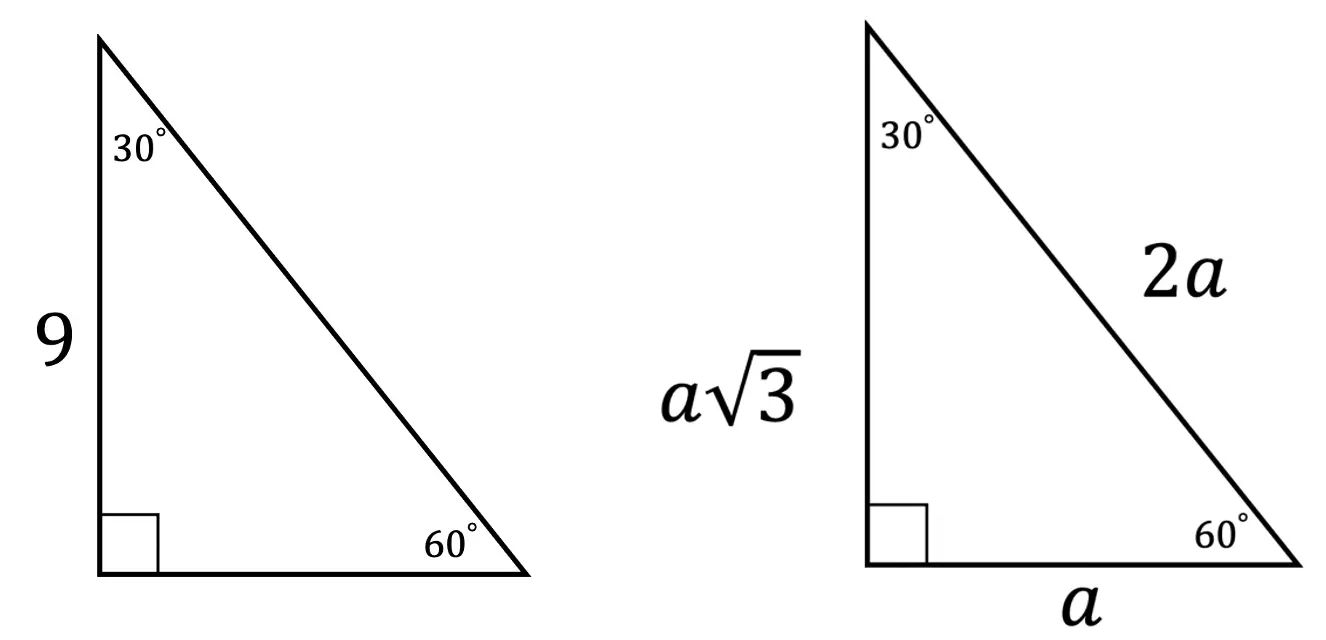



30 60 90 Special Triangles Geometry Mathsux 2




Relationships Of Sides In 30 60 90 Right Triangles Ck 12 Foundation




30 60 90 Triangle Definition Theorem Formula Examples




30 60 90 Right Triangles Read Geometry Ck 12 Foundation



Solve A 30 60 90 Triangle With Gradea



Special Right Triangles
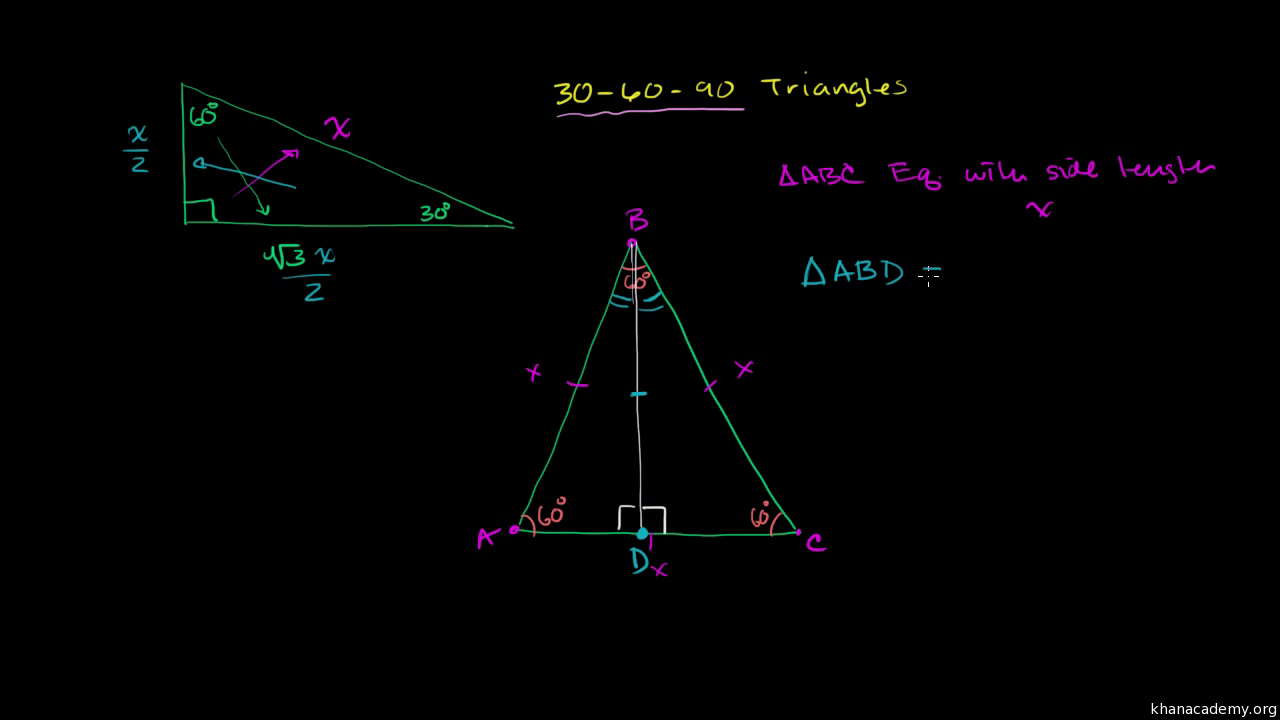



Special Right Triangles Proof Part 1 Video Khan Academy




30 60 90 Right Triangle Side Ratios Expii




30 60 90 Triangle Calculator Formula Rules




30 60 90 Right Triangles Free Math Help



Identifying The 30 60 90 Degree Triangle Dummies



Identifying The 30 60 90 Degree Triangle Dummies




5 30 60 90 Triangles Geometry15a



The Length Of The Hypotenuse Of A 30 60 90 Triangle Is 12cm What Is The Length Of The Longer Leg What Is The Length Of The Shorter Leg Quora



30 60 90 Triangle




Fill In The Blanks In The 30 60 90 Triangle Below Side S Has A Length Of And Side Q Has Brainly Com




30 60 90 Triangle Calculator Formula Rules




30 60 90 Triangle Theorem Ratio Formula Video



30 60 90 Formula Learn Formula For Calculating The 30 60 90 Measures




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com




The Complete Guide To The 30 60 90 Triangle




Fill In The Blanks In The 30 60 90 Triangle Below Side S Has A Length Of And Side R Has A Brainly Com
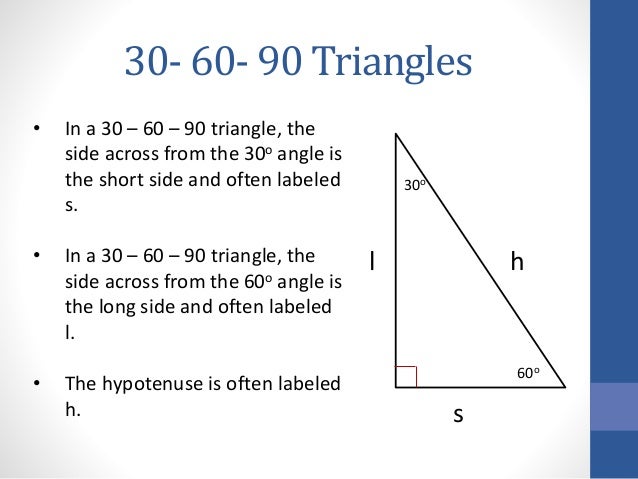



30 60 90 Triangles




Special Right Triangles Video Lessons Examples And Solutions



Tarantamath Licensed For Non Commercial Use Only Razan 10 3
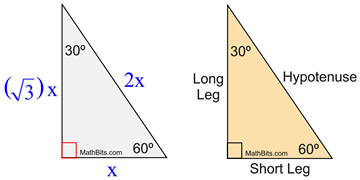



Special Right Triangle 30 60 90 Mathbitsnotebook Geo Ccss Math
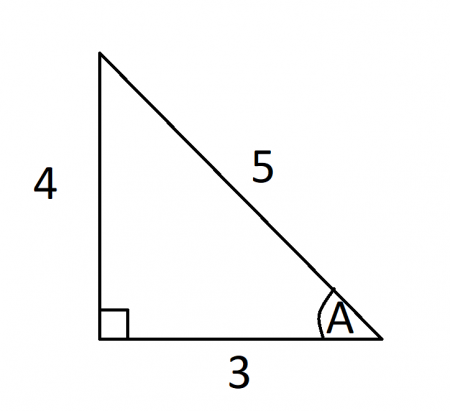



30 60 90 Triangle Formulas Rules And Sides Science Trends



The Easy Guide To The 30 60 90 Triangle
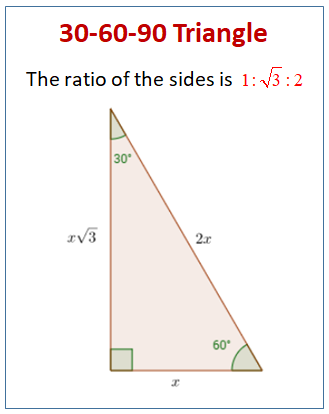



30 60 90 Special Right Triangles Videos Worksheets Examples Solutions




A Quick Guide To The 30 60 90 Degree Triangle Dummies



1




The Complete Guide To The 30 60 90 Triangle




Triangle Gma Is 30 Degree 60 Degree 90 Degree If M 26 Cm Find A And S Study Com



30 60 90 Triangle From Wolfram Mathworld




30 60 90 Triangle Theorem Ratio Formula Video



1




30 60 90 Triangle Theorem Ratio Formula Video




How To Work With 30 60 90 Degree Triangles Education Is Around




He Length Of The Hypotenuse Of A 30 60 90 Triangle Is 13 Meters Find The Length Of The Side Brainly Com




Find Sides Of 45 45 90 30 60 90 Right Triangles Youtube



A 30 60 90 Triangle



Special Right Triangle 30 60 90 Mathbitsnotebook Geo Ccss Math




30 60 90 Triangle Definition Theorem Formula Examples



How Do You Find Missing Sides In A 30a 60a 90a Triangle Virtual Nerd



Trigonometry



In A 30 60 90 Triangle Where The Shortest Leg Equals 3 What Could The Other Sides Equal Socratic



A 30 60 90 Triangle Math Central




30 60 90 Triangle Formulas Rules And Sides Science Trends
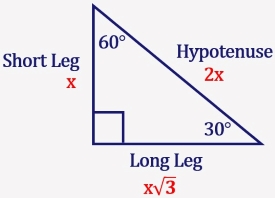



Find The Side Lengths Of A Special Right Triangle 30 60 90 Mathondemand Com
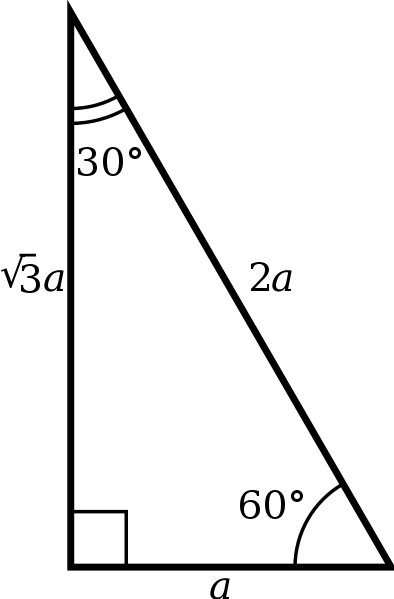



30 60 90 Triangle Formulas Rules And Sides Science Trends




30 60 90 Triangle Geometry Help
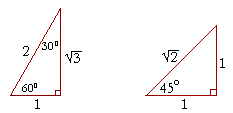



The 30 60 90 Triangle Topics In Trigonometry
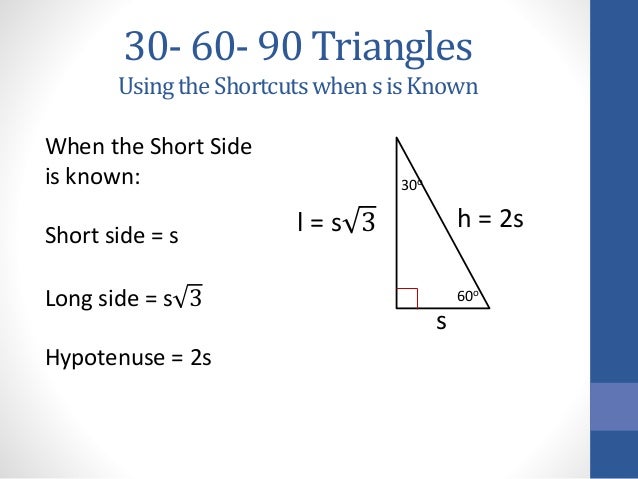



30 60 90 Triangles
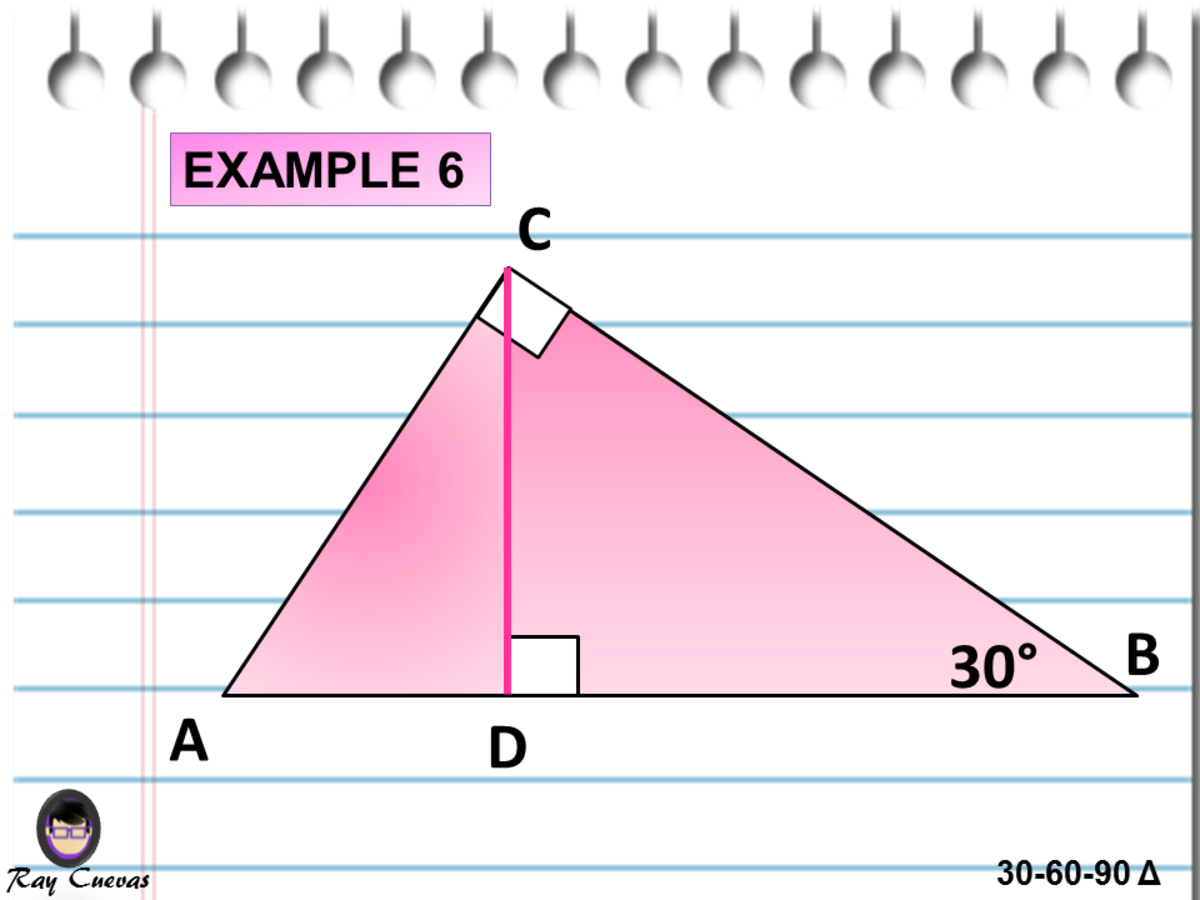



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation
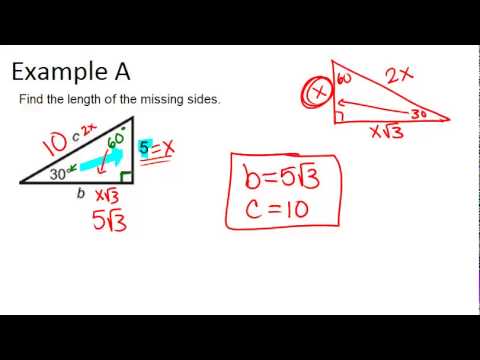



30 60 90 Right Triangles Examples Geometry Concepts Youtube
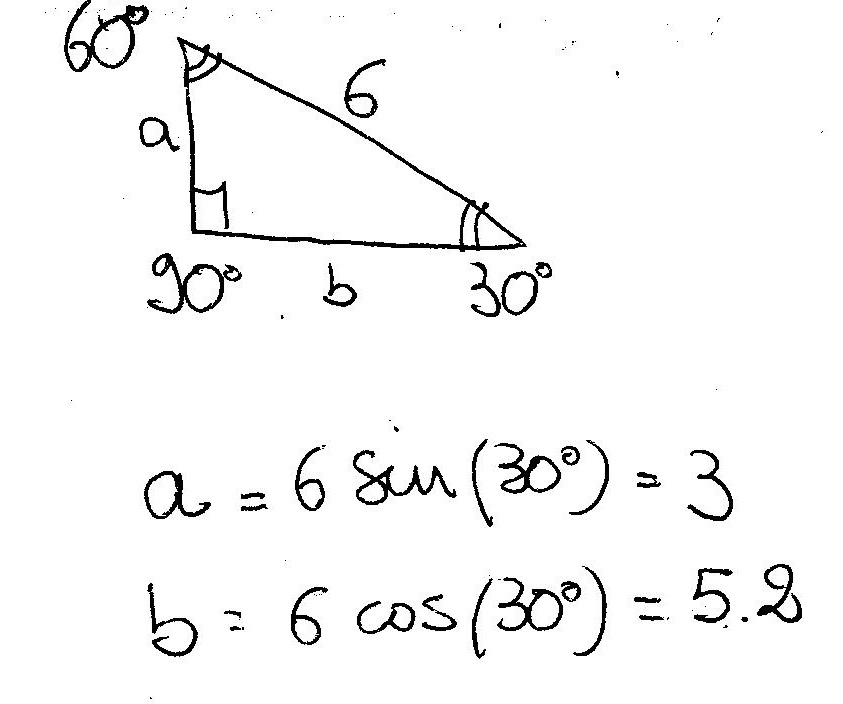



How Do You Find The Remaining Sides Of 30 Circ 60 Circ 90 Circ Triangle If The Longest Side Is 6 Socratic



The Easy Guide To The 30 60 90 Triangle



45 45 90 And 30 60 90 Triangles Zona Land Education
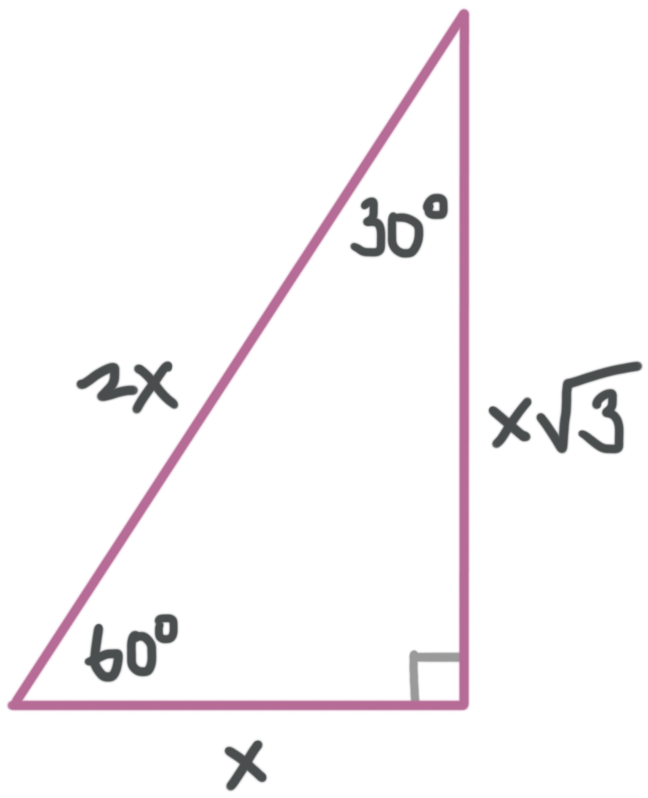



How To Solve 30 60 90 Triangles Krista King Math Online Math Tutor



3



Is A 3 4 5 Triangle Also A 30 60 90 Triangle Quora




30 60 90 Triangle Explanation Examples




Special Right Triangles 30 60 90 And 45 45 90 Triangles Youtube
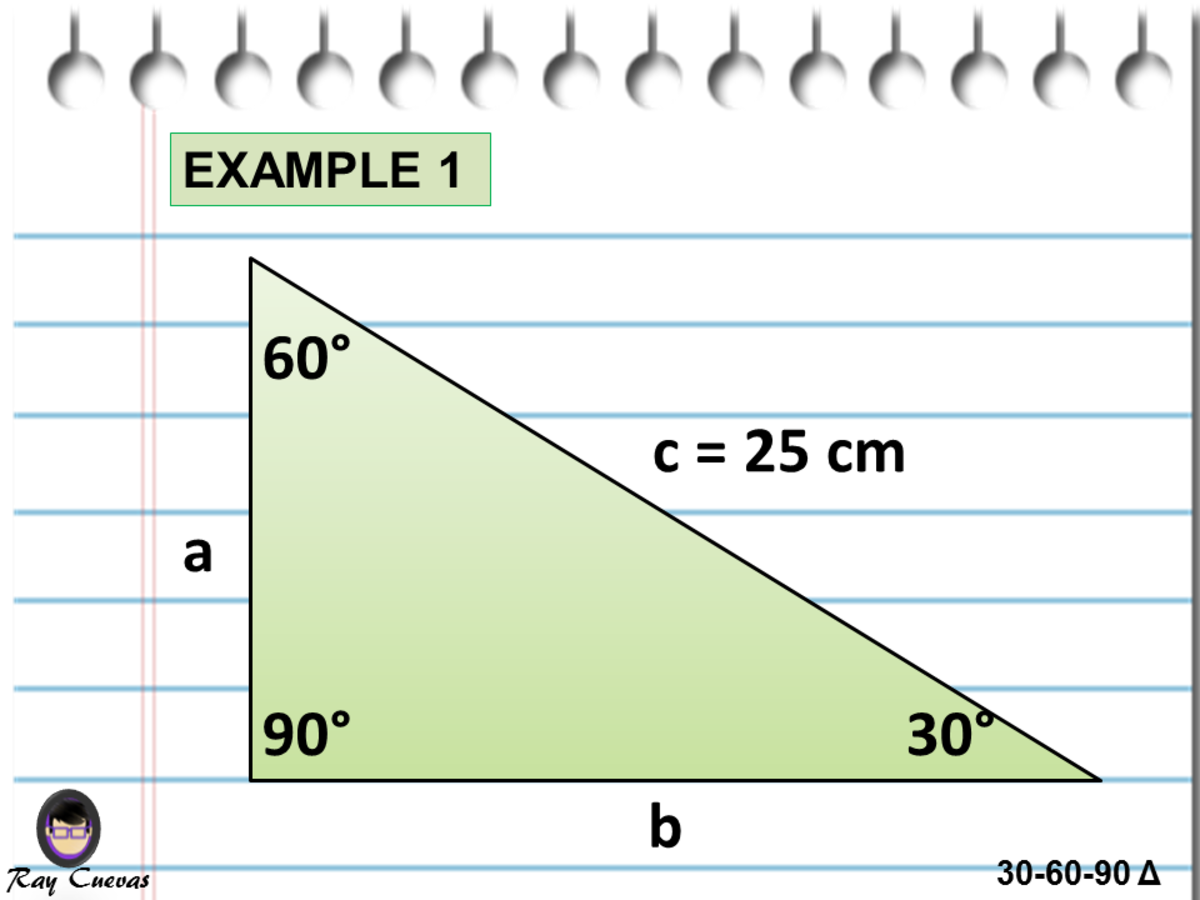



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com




Finding The Missing Side Of 30 60 90 Triangle Youtube
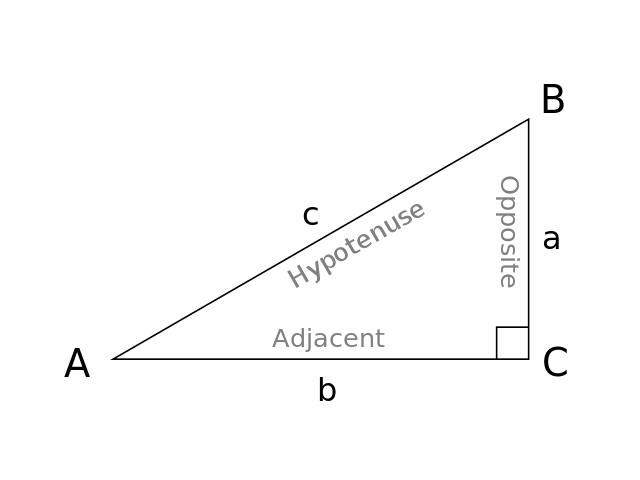



30 60 90 Triangle Formulas Rules And Sides Science Trends




30 60 90 Triangle Theorem Ratio Formula Video




Conquering Right Triangles The Pythagorean Theorem On Act Math Part 1 Magoosh Blog High School



1




5 8b 30 60 90 Special Right Triangles Youtube




30 60 90 Triangle Definition Theorem Formula Examples




30 60 90 Triangle Explanation Examples




30 60 90 Triangle Calculator Formula Rules



0 件のコメント:
コメントを投稿